2.1.2. Dynamical Systems Library (DynSysLib)

:math:`x`-solution to simulated Rössler system for a chaotic response.

This page provides a summary of the Dynamical Systems Library (DynSysLib) for simulating a wide variety of dynamical systems.

The following table provides a list of all the available dynamical systems. Further details for each system can be found in the linked directories.

Table 2.1 Available Dynamical Systems
Maps	Autonomous Dissipative Flows	Driven Dissipative Flows	Conservative Flows	Periodic Functions	Noise Models	Medical Data	Delayed Flows
logistic_map	chua	driven_pendulum	driven_van_der_pol_oscillator	sine	gaussian_noise	ECG	mackey_glass
henon_map	lorenz	shaw_van_der_pol_oscillator	simplest_driven_chaotic_flow	incommensurate_sine	uniform_noise	EEG
sine_map	rossler	forced_brusselator	nose_hoover_oscillator		rayleigh_noise
tent_map	coupled_lorenz_rossler	ueda_oscillator	labyrinth_chaos		exponential_noise
linear_congruential_generator_map	coupled_rossler_rossler	duffings_two_well_oscillator	henon_heiles_system
rickers_population_map	double_pendulum	duffing_van_der_pol_oscillator
gauss_map	diffusionless_lorenz_attractor	rayleigh_duffing_oscillator
cusp_map	complex_butterfly
pinchers_map	chens_system
sine_circle_map	hadley_circulation
lozi_map	ACT_attractor
delayed_logstic_map	rabinovich_frabrikant_attractor
tinkerbell_map	linear_feedback_rigid_body_motion_system
burgers_map	moore_spiegel_oscillator
holmes_cubic_map	thomas_cyclically_symmetric_attractor
kaplan_yorke_map	halvorsens_cyclically_symmetric_attractor
ginger_bread_man_map	burke_shaw_attractor
	rucklidge_attractor
	WINDMI
	simplest_quadratic_chaotic_flow
	simplest_cubic_chaotic_flow
	simplest_piecewise_linear_chaotic_flow
	double_scroll

Of the optional other parameters either the dynamic_state parameter or the system parameters must be used.

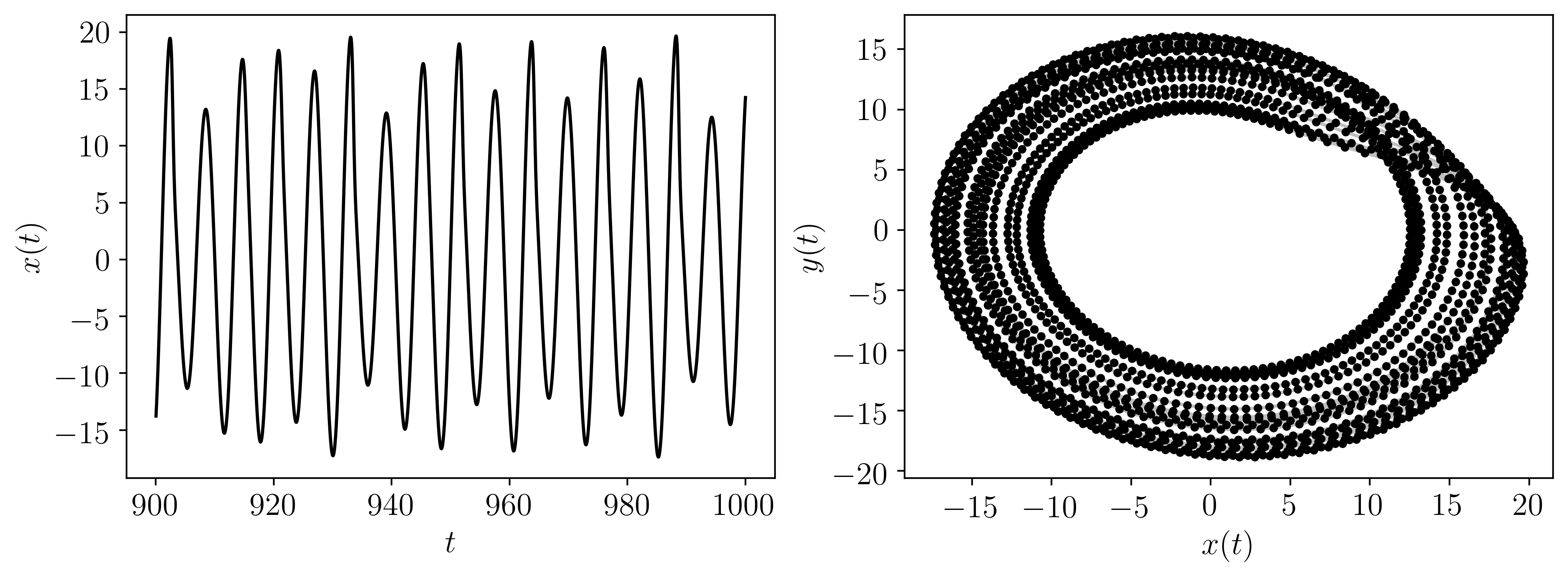
The following is a minimal working example using the rossler system:

import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
from teaspoon.MakeData.DynSysLib.autonomous_dissipative_flows import rossler

t, ts = rossler(dynamic_state='periodic')

TextSize = 15
plt.figure(figsize = (12,4))
gs = gridspec.GridSpec(1,2)

ax = plt.subplot(gs[0, 0])
plt.xticks(size = TextSize)
plt.yticks(size = TextSize)
plt.ylabel(r'$x(t)$', size = TextSize)
plt.xlabel(r'$t$', size = TextSize)
plt.plot(t,ts[0], 'k')

ax = plt.subplot(gs[0, 1])
plt.plot(ts[0], ts[1],'k.')
plt.plot(ts[0], ts[1],'k', alpha = 0.25)
plt.xticks(size = TextSize)
plt.yticks(size = TextSize)
plt.xlabel(r'$x(t)$', size = TextSize)
plt.ylabel(r'$y(t)$', size = TextSize)

plt.show()

Where the output for this example is:

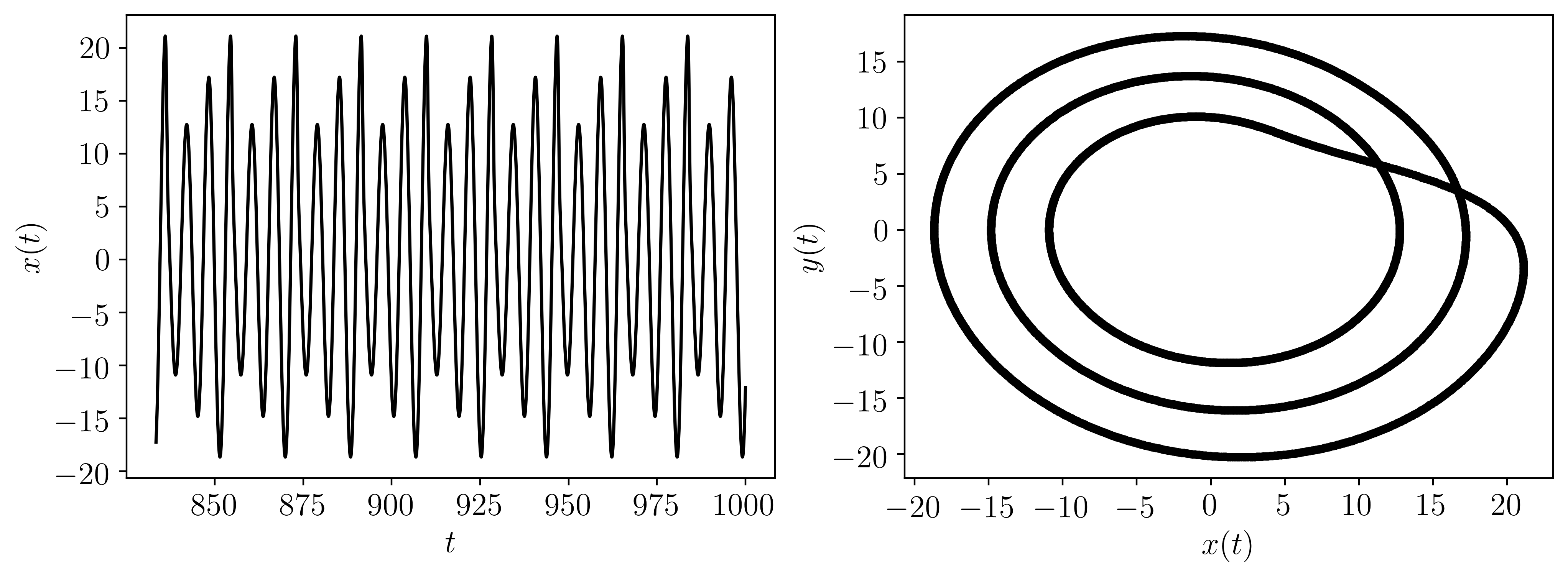
The following is another example implementing all of the possible inputs (dynamic_state is not needed when parameters are provided):

import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
from teaspoon.MakeData.DynSysLib.autonomous_dissipative_flows import rossler


L, fs, SampleSize = 1000, 20, 2000

# the length (in seconds) of the time series, the sample rate, and the sample size of the time series of the simulated system.

parameters = [0.1, 0.2, 13.0] # these are the a, b, and c parameters from the Rossler system model.

InitialConditions = [1.0, 0.0, 0.0] # [x_0, y_0, x_0]

t, ts = rossler(L=L, fs=fs, SampleSize=SampleSize, parameters=parameters,  InitialConditions=InitialConditions)

TextSize = 15
plt.figure(figsize = (12,4))
gs = gridspec.GridSpec(1,2)

ax = plt.subplot(gs[0, 0])
plt.xticks(size = TextSize)
plt.yticks(size = TextSize)
plt.ylabel(r'$x(t)$', size = TextSize)
plt.xlabel(r'$t$', size = TextSize)
plt.plot(t,ts[0], 'k')

ax = plt.subplot(gs[0, 1])
plt.plot(ts[0], ts[1],'k.')
plt.plot(ts[0], ts[1],'k', alpha = 0.25)
plt.xticks(size = TextSize)
plt.yticks(size = TextSize)
plt.xlabel(r'$x(t)$', size = TextSize)
plt.ylabel(r'$y(t)$', size = TextSize)

plt.show()

Where the output for this example is: