2.1.2.8. Delayed Flows

2.1.2.8.1. Main Functions

teaspoon.MakeData.DynSysLib.delayed_flows.mackey_glass(parameters=[1.0001, 2.0, 2.0, 7.75], fs=5, SampleSize=1000, L=400, dynamic_state=None)

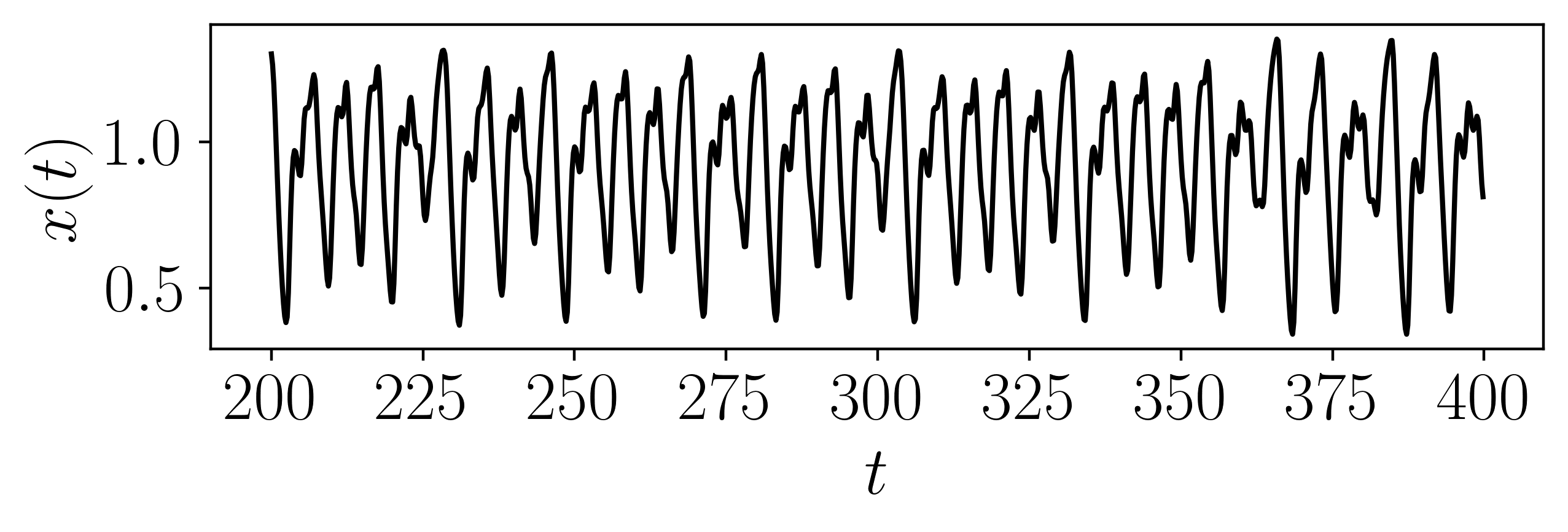
The Mackey-Glass Delayed Differential Equation is

\[\dot{x}(t) = -\gamma*x(t) + \beta*\frac{x(t - \tau)}{1 + x(t - \tau)^n}\]

where we chose the parameters \(\tau = 2, \beta = 2, \gamma = 1,\) and \(n = 9.65\). We solve this system for 400 seconds with a sampling rate of 50 Hz. The solution was then downsampled to 5 Hz and the last 200 seconds were used for the figure.

Parameters:

• parameters (Optional[floats]) – Array of four floats [gamma, tau, beta, n] or None if using the dynamic_state variable

• fs (Optional[float]) – Sampling rate for simulation

• SampleSize (Optional[int]) – length of sample at end of entire time series

• L (Optional[int]) – Number of iterations

• dynamic_state (Optional[str]) – Set dynamic state as either ‘periodic’ or ‘chaotic’ if not supplying parameters.

Returns:

Array of the time indices as t and the simulation time series ts

Return type:

array