2.3.1. Time Series Analysis (TSA) Tools
The following are the available TSA functions:
Further detailed documentation and examples are provided below for each (or click link).
2.3.1.1. Takens’ Embedding
The Takens’ embedding algorhtm reconstructs the state space from a single time series with delay-coordinate embedding as shown in the animation below.
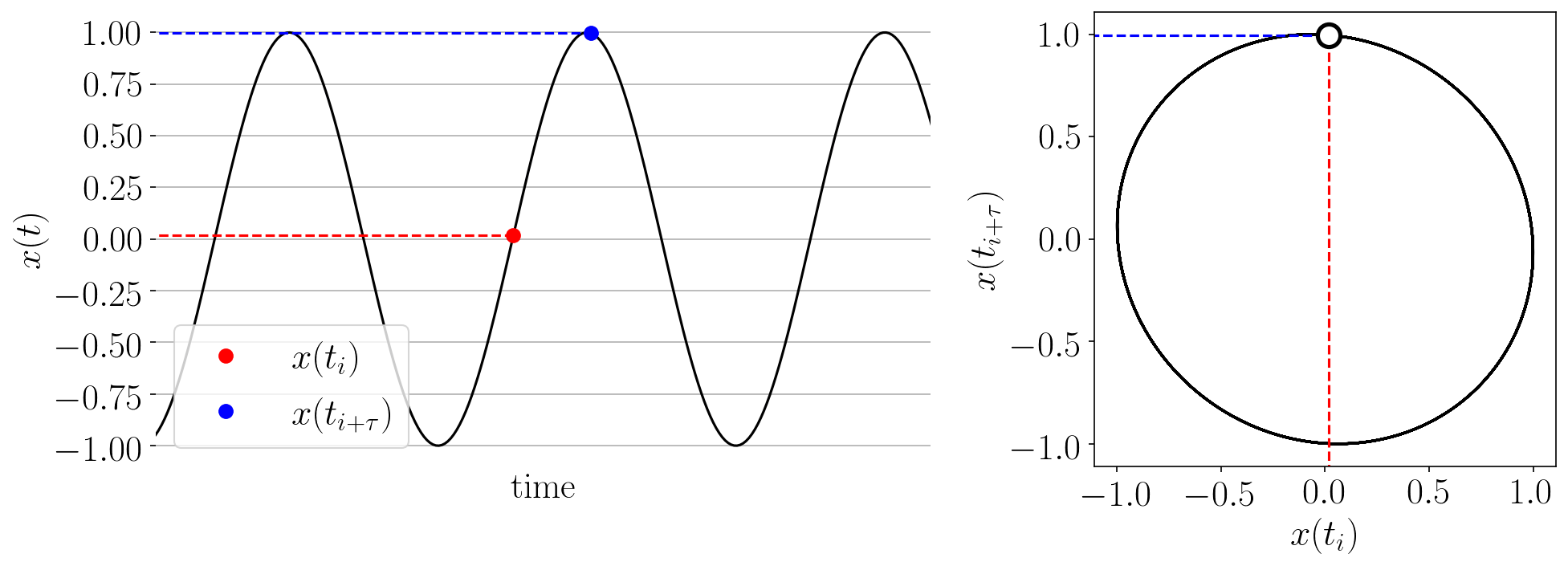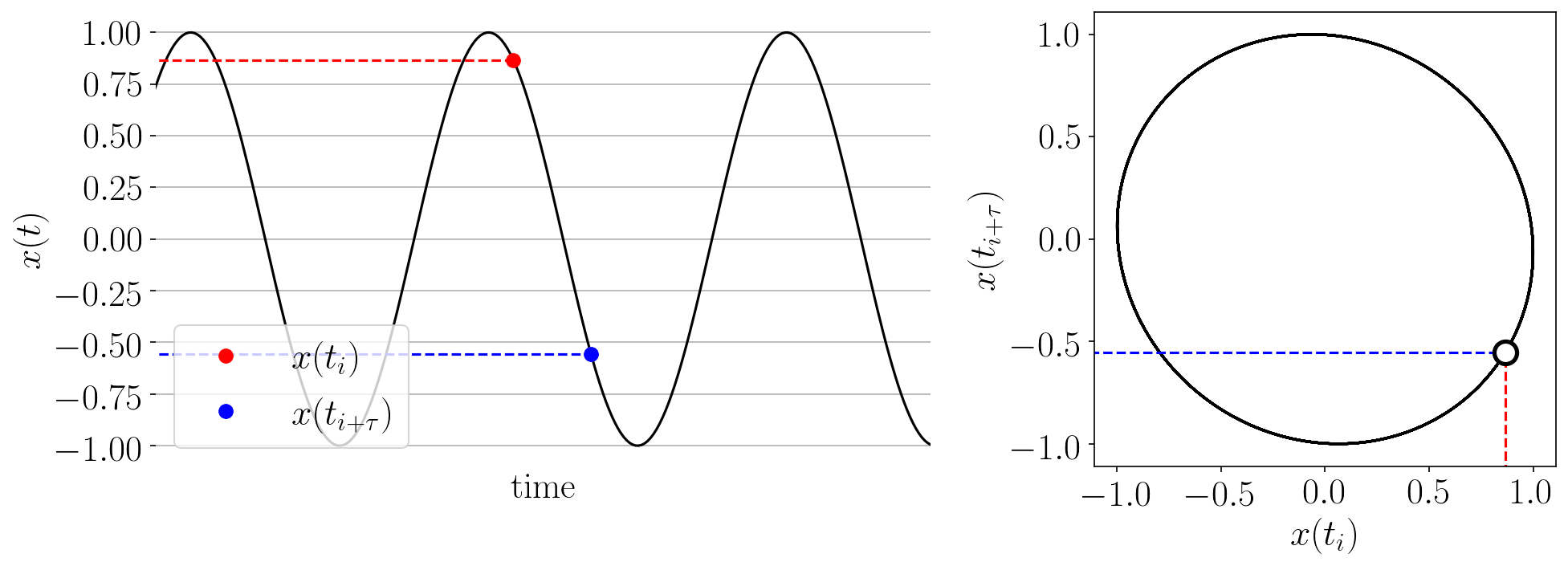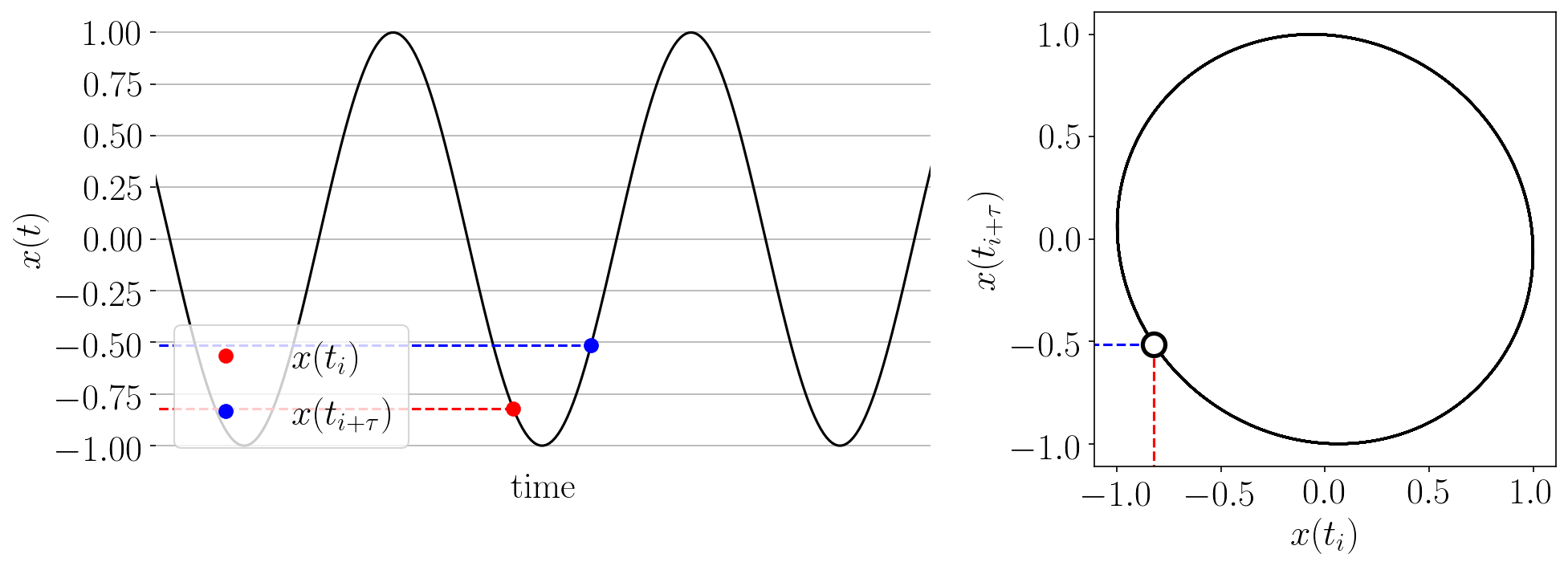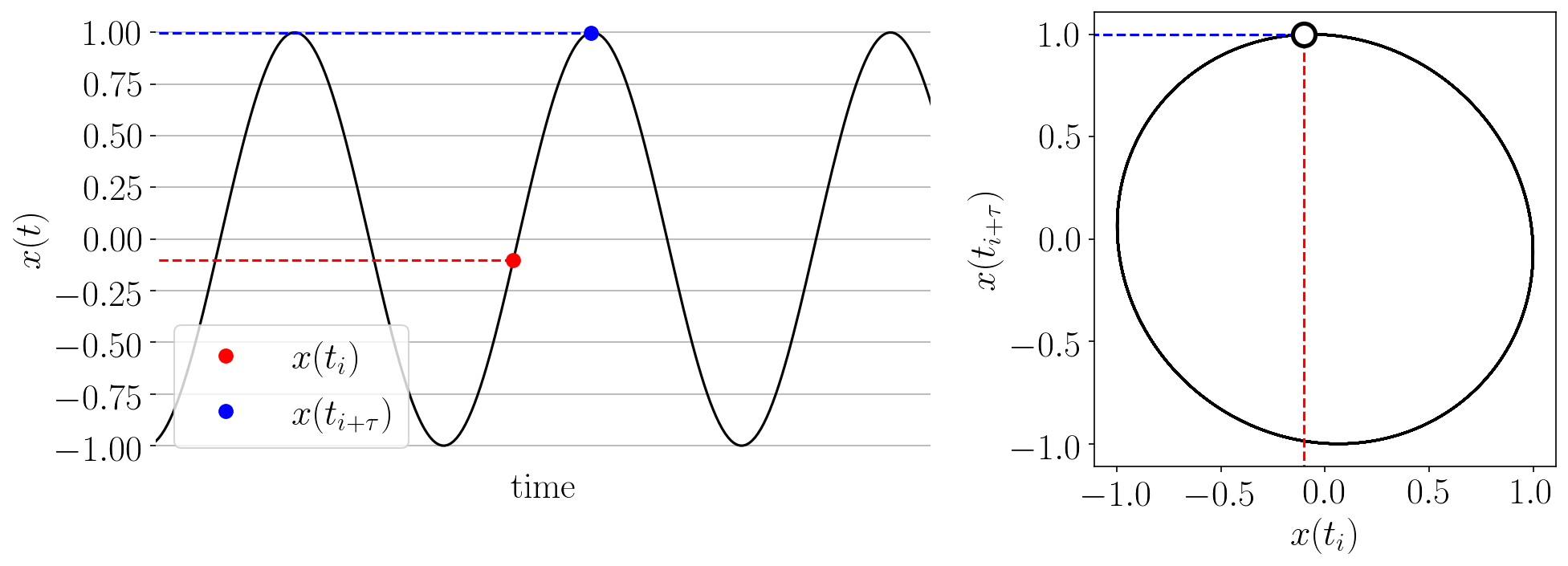
Figure: Takens’ embedding animation for a simple time series and embedding of dimension two. This embeds the 1-D signal into n=2 dimensions with delayed coordinates.
- teaspoon.SP.tsa_tools.takens(ts, n=None, tau=None)[source]
This function generates an array of n-dimensional arrays from a time-delay state-space reconstruction.
- Parameters:
ts (1-D array) – 1-D time series signal
n (Optional[int]) – embedding dimension for state space reconstruction. Default is uses FNN algorithm from parameter_selection module.
tau (Optional[int]) – embedding delay fro state space reconstruction. Default uses MI algorithm from parameter_selection module.
- Returns:
array of delyed embedded vectors of dimension n for state space reconstruction.
- Return type:
[arraay of n-dimensional arrays]
The two parameters needed for state space reconstruction (Takens’ embedding) are the delay parameter and dimension parameter. These can be selected automatically from the parameter selection module ( Parameter selection module documentation).
Example:
import numpy as np
t = np.linspace(0,30,200)
ts = np.sin(t) #generate a simple time series
from teaspoon.SP.tsa_tools import takens
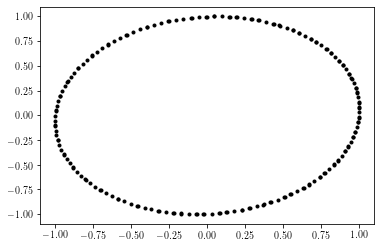
embedded_ts = takens(ts, n = 2, tau = 10)
import matplotlib.pyplot as plt
plt.plot(embedded_ts.T[0], embedded_ts.T[1], 'k.')
plt. show()
Output of example:
2.3.1.2. Permutation Sequence Generation
The function provides an array of the permutations found throughout the time series as shown in the
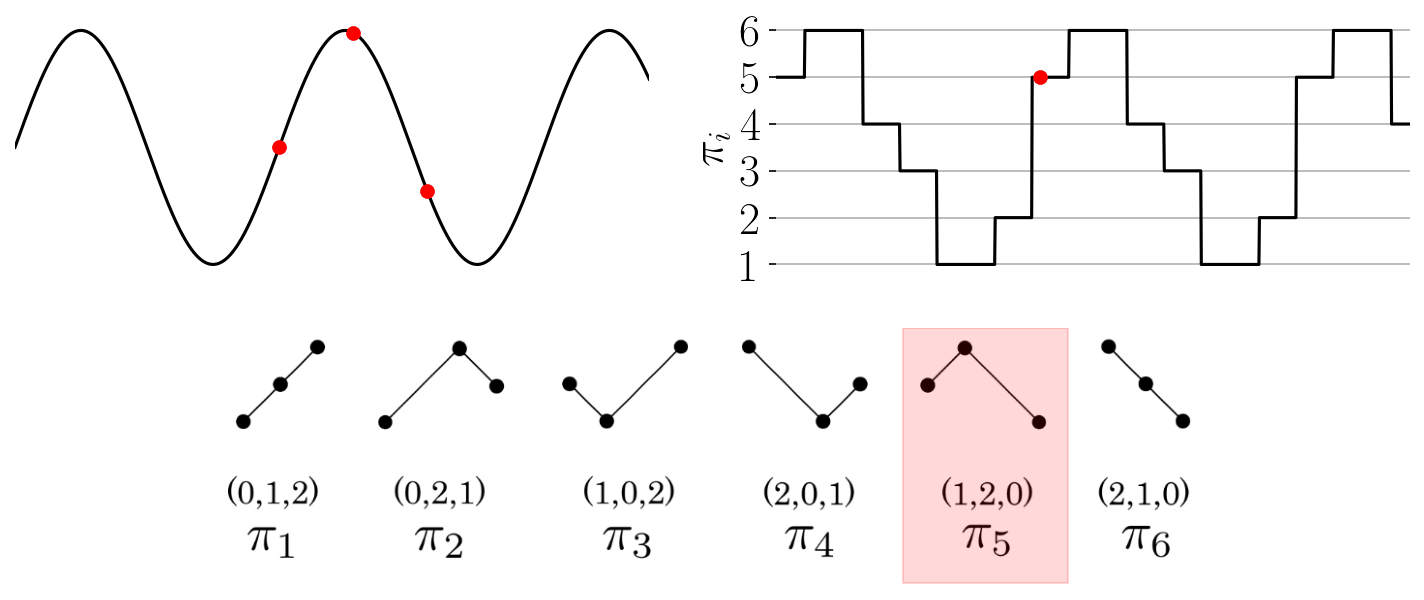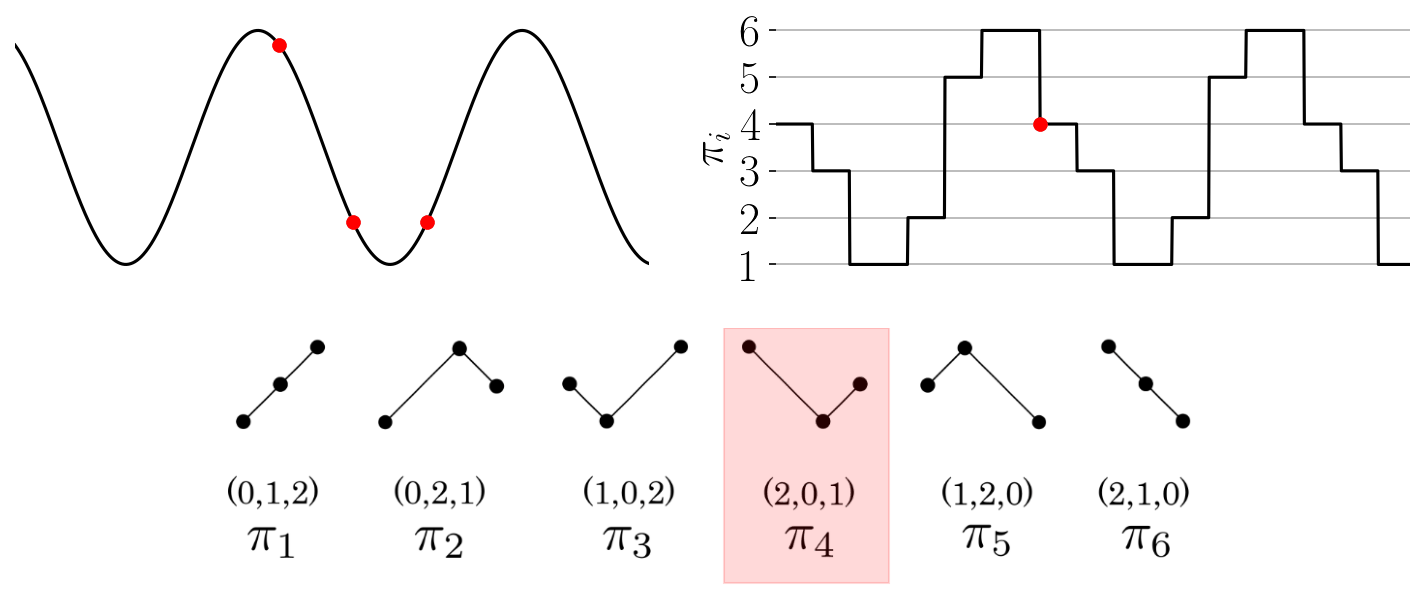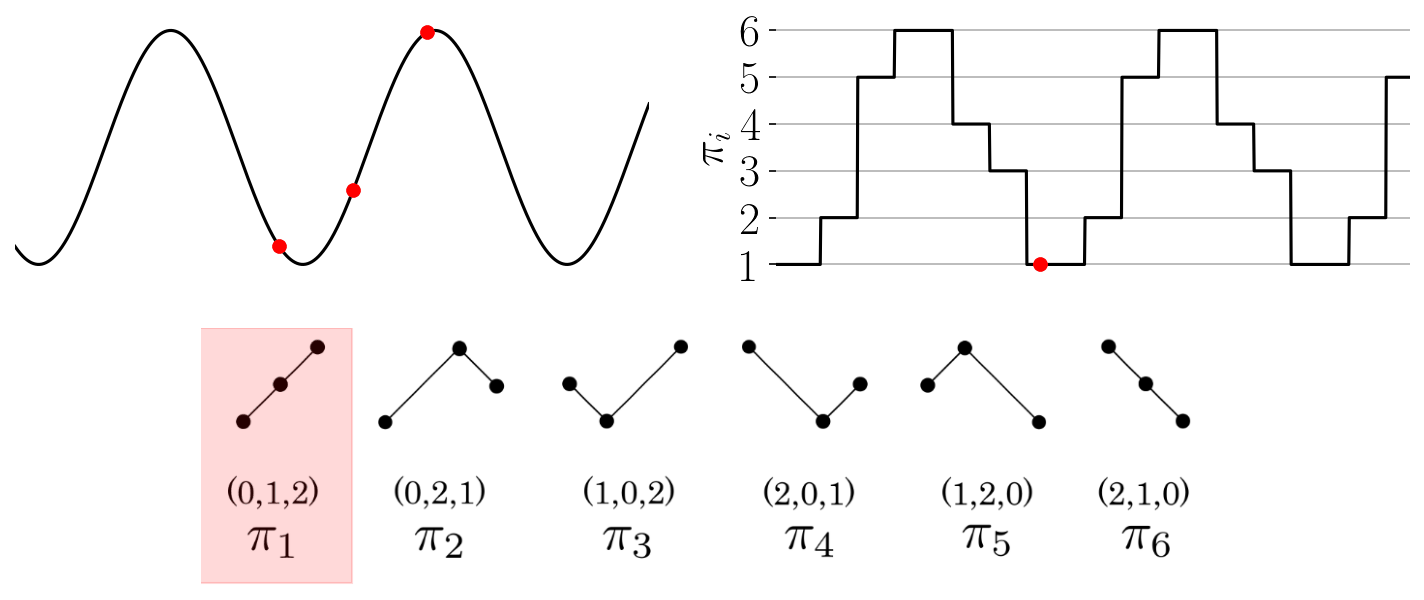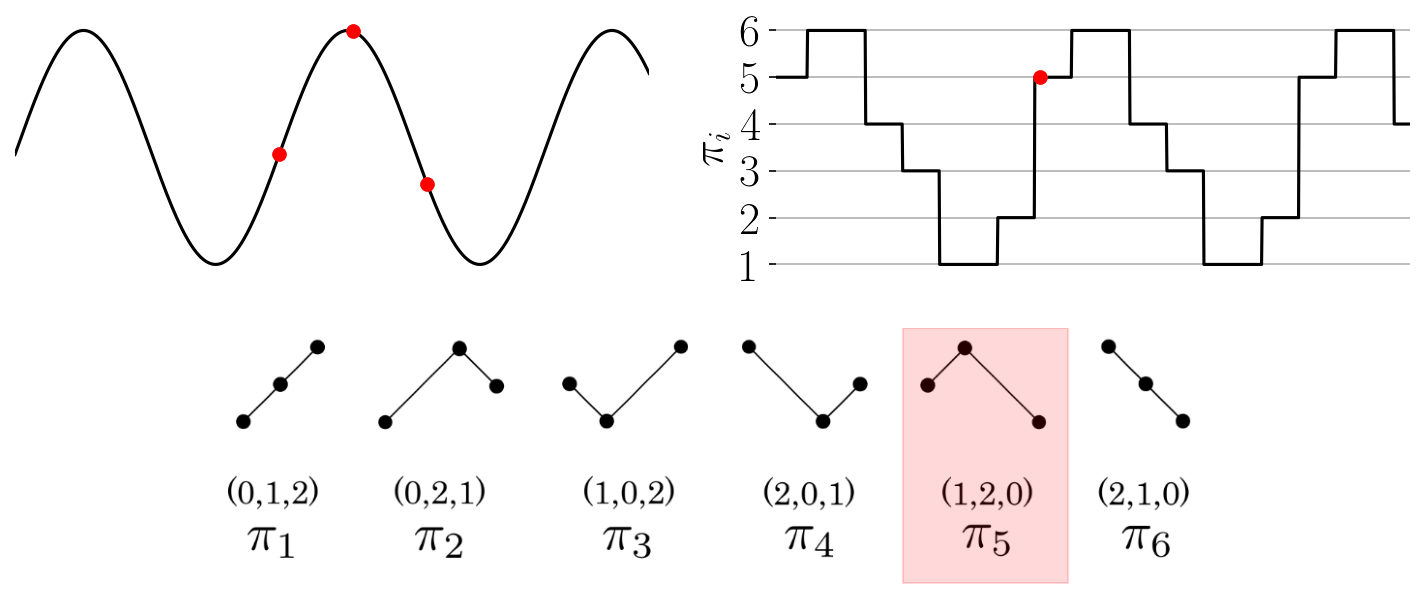
Figure: Permutation sequence animation for a simple time series and permutations of dimension three.
- teaspoon.SP.tsa_tools.permutation_sequence(ts, n=None, tau=None)[source]
This function generates the sequence of permutations from a 1-D time series.
- Parameters:
ts (1-D array) – 1-D time series signal
n (Optional[int]) – embedding dimension for state space reconstruction. Default is uses MsPE algorithm from parameter_selection module.
tau (Optional[int]) – embedding delay fro state space reconstruction. Default uses MsPE algorithm from parameter_selection module.
- Returns:
array of permutations represented as int from [0, n!-1] from the time series.
- Return type:
[1-D array of intsegers]
The two parameters needed for permutations are the delay parameter and dimension parameter. These can be selected automatically from the parameter selection module ( Parameter selection module documentation).
Example:
import numpy as np
t = np.linspace(0,30,200)
ts = np.sin(t) #generate a simple time series
from teaspoon.SP.tsa_tools import permutation_sequence
PS = permutation_sequence(ts, n = 3, tau = 12)
import matplotlib.pyplot as plt
plt.plot(t[:len(PS)], PS, 'k')
plt. show()
Output of example:

2.3.1.3. k Nearest Neighbors
- teaspoon.SP.tsa_tools.k_NN(embedded_time_series, k=4)[source]
This function gets the k nearest neighbors from an array of the state space reconstruction vectors
- Parameters:
embedded_time_series (array of n-dimensional arrays) – state space reconstructions vectors of dimension n. Can use takens function.
k (Optional[int]) – number of nearest neighbors for graph formation. Default is 4.
- Returns:
distances and indices of the k nearest neighbors for each vector.
- Return type:
[distances, indices]
Example:
import numpy as np
t = np.linspace(0,15,100)
ts = np.sin(t) #generate a simple time series
from teaspoon.SP.tsa_tools import takens
embedded_ts = takens(ts, n = 2, tau = 10)
from teaspoon.SP.tsa_tools import k_NN
distances, indices = k_NN(embedded_ts, k=4)
import matplotlib.pyplot as plt
plt.plot(embedded_ts.T[0], embedded_ts.T[1], 'k.')
i = 20 #choose arbitrary index to get NN of.
NN = indices[i][1:] #get nearest neighbors of point with that index.
plt.plot(embedded_ts.T[0][NN], embedded_ts.T[1][NN], 'rs') #plot NN
plt.plot(embedded_ts.T[0][i], embedded_ts.T[1][i], 'bd') #plot point of interest
plt. show()
Output of example:

2.3.1.4. Coarse grained state space binning
Please reference publication “Persistent Homology of the Coarse Grained State Space Network” for details.
- teaspoon.SP.tsa_tools.cgss_binning(ts, n=None, tau=None, b=12, binning_method='equal_size', plot_binning=False)[source]
This function generates the binning array applied to each dimension when constructing CGSSN.
- Parameters:
ts (1-D array) – 1-D time series signal
n (Optional[int]) – embedding dimension for state space reconstruction. Default is uses MsPE algorithm from parameter_selection module.
tau (Optional[int]) – embedding delay from state space reconstruction. Default uses FNN algorithm from parameter_selection module.
b (Optional[int]) – Number of bins per dimension. Default is 12.
plot_binning (Optional[bool]) – Option to display plotting of binning over space occupied by SSR. default is False.
binning_method (Optional[str]) – Either equal_size or equal_probability for creating binning array. Default is equal_size.
- Returns:
One-dimensional array of bin edges.
- Return type:
[1-D array]
2.3.1.5. Coarse grained state space state sequence
Please reference publication “Persistent Homology of the Coarse Grained State Space Network” for details.
- teaspoon.SP.tsa_tools.cgss_sequence(SSR, B_array)[source]
This function generates the sequence of coarse-grained state space states from the state space reconstruction.
- Parameters:
SSR (n-D array) – n-dimensional state state space reconstruction using takens function from teaspoon.
B_array (1-D array) – binning array from function cgss_binning or self defined. Array of bin edges applied to each dimension of SSR for CGSS state sequence.
- Returns:
array of coarse grained state space states represented as ints.
- Return type:
[1-D array of integers]
2.3.1.6. Zero Detection Algorithm (ZeDA)
This section provides a summary of the zero-crossing detection algorithm devised and analysed in “Robust Zero-crossings Detection in Noisy Signals using Topological Signal Processing” for discrete time series. Additionally, a basic example is provided showing the functionality of the method for a simple time series. Below, a simple overview of the method is provided.
Outline of method: a time series is converted to two point clouds \((P)\) and \((Q)\) based on the sign value. A sorted persistence diagram is generated for both point clouds with \(x\)-axis having the index of the data point and \(y\)-axis having the death values. Then, a persistence threshold or an outlier detection method is used to select the outlying points in the persistence diagram such that \(n+1\) points correspond to \(n\) brackets.

- teaspoon.SP.tsa_tools.ZeDA(sig, t1, tn, level=0.0, plotting=False, method='std', score=3.0)[source]
This function takes a uniformly sampled time series and finds level-crossings.
- Parameters:
sig (numpy array) – Time series (1d) in format of npy.
t1 (float) – Initial time of recording signal.
tn (float) – Final time of recording signal.
level (Optional[float]) – Level at which crossings are to be found; default: 0.0 for zero-crossings
plotting (Optional[bool]) – Plots the function with returned brackets; defaut is False.
method (Optional[str]) – Method to use for setting persistence threshold; ‘std’ for standard deviation, ‘iso’ for isolation forest, ‘dt’ for smallest time interval in case of a clean signal; default is std (3*standard deviation)
score (Optional[float]) – z-score to use if method == ‘std’; default is 3.0
- Returns:
brackets gives intervals in the form of tuples where a crossing is expected; crossings gives the estimated crossings in each interval obtained by averaging both ends; flags marks, for each interval, whether both ends belong to the same sgn(function) category (0, unflagged; 1, flagged)
- Return type:
[tuples, list, list]
Example:
import numpy as np
t1 = 0 # Initial time value
tn = 1.2 # Final time value
t = np.linspace(t1, tn, 200, endpoint=True) # Generate a time array
sig = (-3*t + 1.4)*np.sin(18*t) + 0.1 # Generate a time series
from teaspoon.SP.tsa_tools import ZeDA
brackets, ZC, flag = ZeDA(sig, t1, tn, plotting=True)
Output of example:

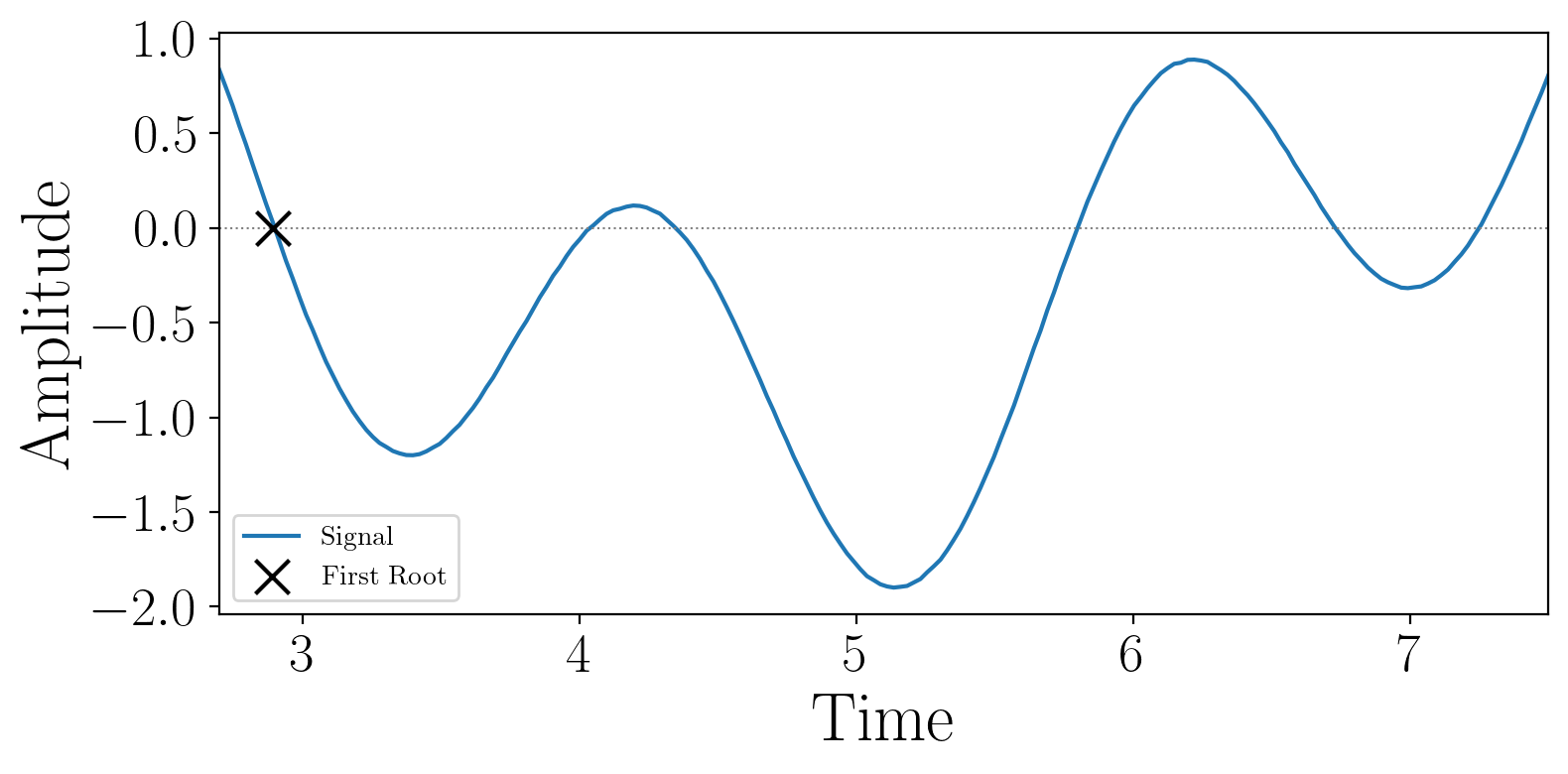
2.3.1.7. First Zero Detection Algorithm
This section provides an implementation of a zero-crossing detection algorithm for the first zero (or the global minimum) in the interval given a discrete time series. This was proposed in “An efficient algorithm for the zero crossing detection in digitized measurement signal”, and was used for benchmarking the algorithm ZeDA above.
- teaspoon.SP.tsa_tools.first_zero(sig, t1, tn, level=0.0, r=1.2, plotting=False)[source]
This function takes a discrete time series and finds the first zero-crossing or the global minimum (if no crossing).
- Parameters:
sig (numpy array) – Time series (1d) in format of npy.
t1 (float) – Initial time of recording signal.
tn (float) – Final time of recording signal.
level (Optional[float]) – Level at which crossings are to be found; default: 0.0 for zero-crossings
r (Optional[float]) – Reliability (>0)–increasing r increases reliability of the method but may result in a higher convergence time; default: 1.2
plotting (Optional[bool]) – Plots the function with returned brackets; defaut is False.
- Returns:
the estimated first crossing in the interval or the global minimum.
- Return type:
float
Example:
import numpy as np
t1 = 2.7 # Initial time value
tn = 7.5 # Final time value
t = np.linspace(t1, tn, 200, endpoint=True) # Generate a time array
sig = (-3*t + 1.4)*np.sin(18*t) + 0.1 # Generate a time series
from teaspoon.SP.tsa_tools import first_zero
ZC = first_zero(sig, t1, tn, plotting=True)
Output of example: