2.1.1. Bifurcations using ZigZag (BuZZ)

This module contains code for the Bifurcations using ZigZag (BuZZ) method, which uses zigzag persistence to detect parameter values in a dynamical system which have a Hopf bifurcation. The paper summarizing this methodology is “Using Zigzag Persistent Homology to Detect Hopf Bifurcations in Dynamical Systems”. A basic example showing the functionality for some synthetic time series data can be found below.

class sporktda.TDA.BuZZ.PtClouds(ptclouds, cplx_type='rips', num_landmarks=None, verbose=False)[source]

Class to hold collection of point clouds.

Parameters:

  • ptclouds (list) – List of point clouds

  • cplx_type (string (not case sensitive)) – Type of complex you want to use. Options are Rips or Landmark (default is Rips)

  • num_landmarks (int) – Number of points to subsample (default is None, meaning no subsampling)

  • verbose (bool) – If true, prints updates when running code (default is False)

plot_ZZ_Cplx(save=False, savename='Cplx.png', v_plts=None, h_plts=None)[source]

Plot the zigzag of rips complexes.

Parameters:

  • save (bool) – Set to true if you want to save the figure (default is False)

  • savename (string) – Path to save figure (default is ‘Cplx.png’ in current directory)

  • v_plts (int) – Number of plots in vertical direction

  • h_plts (int) – Number of plots in horizontal direction

plot_ZZ_Full_PtClouds(save=False, savename='PC_Full.png', v_plts=None, h_plts=None)[source]

Plot the zigzag of full point clouds. Only needed if using landmark complex and want to plot the full point clouds before subsampling.

Parameters:

  • save (bool) – Set to true if you want to save the figure (default is False)

  • savename (string) – Path to save figure (default is ‘PC_Full.png’ in current directory)

  • v_plts (int) – Number of plots in vertical direction

  • h_plts (int) – Number of plots in horizontal direction

plot_ZZ_PtClouds(save=False, savename='PC.png', v_plts=None, h_plts=None)[source]

Plot the zigzag of point clouds.

Parameters:

  • save (bool) – Set to true if you want to save the figure (default is False)

  • savename (string) – Path to save figure (default is ‘PC.png’ in current directory)

  • v_plts (int) – Number of plots in vertical direction

  • h_plts (int) – Number of plots in horizontal direction

run_Zigzag(r, k=2)[source]

Runs zigzag persistence on collections of point clouds, taking unions between each adjacent pair of point clouds. Adds attributes to class zz, zz_dgms, zz_cells which are the outputs of dionysus’ zigzag persistence function. Also adds attributes setup_time and zigzag_time with timing data.

Parameters:

  • r (float or list of floats,) – Parameter for Rips complex on each point cloud. Can be a single number or a list with one value per point cloud.

  • k (int, optional) – Maximum dimension simplex desired (default is 2)

setup_Zigzag_changing(r, k=2, verbose=False)[source]

Helper function for run_Zigzag that sets up inputs needed for Dionysus’ zigzag persistence function. This one allows r to be a list of radii, rather than one fixed value

Parameters:

  • r (list) – List of radii for rips complex of each X_i

  • k (int, optional) – Max dimension for rips complex (default is 2)

  • verbose (bool, optional) – If true, prints updates when running code

Returns:

  • filtration (dio.Filtration) – Dionysis filtration containing all simplices that exist in zigzag sequence

  • times (list) – List of times, where times[i] is a list containing [a,b] where simplex i appears at time a, and disappears at time b

setup_Zigzag_fixed(r, k=2, verbose=False)[source]

Helper function for run_Zigzag that sets up inputs needed for Dionysus’ zigzag persistence function. This only works for a fixed radius r.

Parameters:

  • r (float) – Radius for rips complex

  • k (int, optional) – Max dimension for rips complex (default is 2)

  • verbose (bool, optional) – If true, prints updates when running code

Returns:

  • filtration (dio.Filtration) – Dionysis filtration containing all simplices that exist in zigzag sequence

  • times (list) – List of times, where times[i] is a list containing [a,b] where simplex i appears at time a, and disappears at time b

use_Landmarks(num_landmarks=None)[source]

Uses landmark complex by subsampling each point cloud using a max min approach.

Parameters:

num_landmarks (int) – Number of points to subsample (default is None, meaning no subsampling)

2.1.1.1. Example

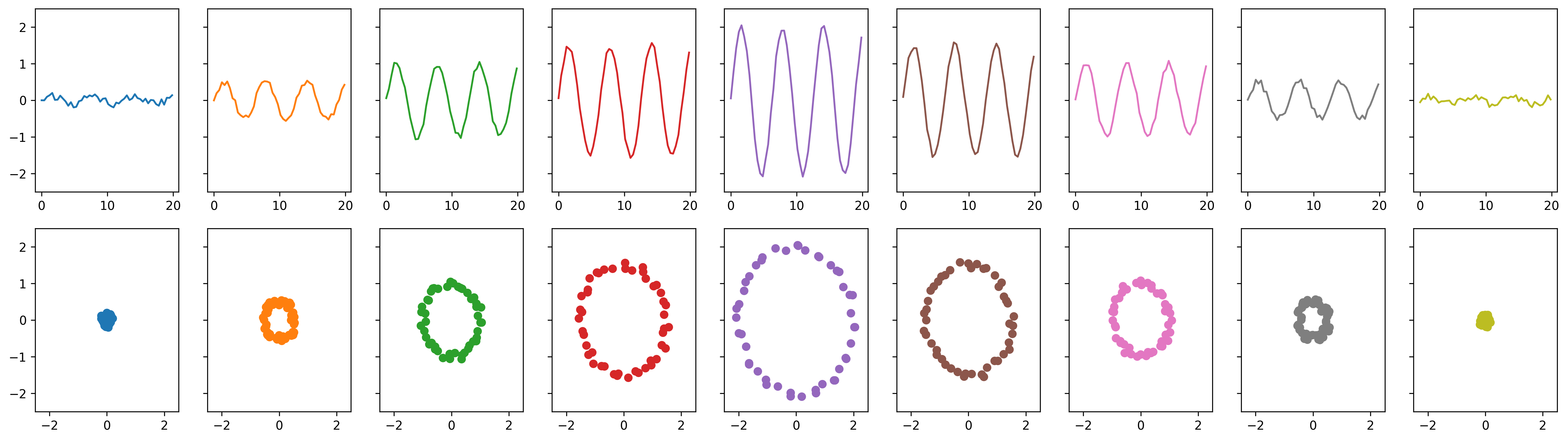
First, import necessary modules, create some example data, and plot it:

import numpy as np
import matplotlib.pyplot as plt
from teaspoon.TDA.Draw import drawDgm
from sporktda.TDA.BuZZ import PtClouds
from teaspoon.SP.tsa_tools import takens

t = np.linspace(0, 6*np.pi+1, 50)

# Amplitudes of sine waves
amps = [0.1,0.5,1,1.5,2,1.5,1,0.5,0.1]

ts_list = []
ptcloud_list = []
for a in amps:
    y = a*np.sin(t) + (0.1*np.random.randint(-100,100,len(t))/100)

    # Compute sine wave and add noise uniformly distributed in [-0.1, 0.1]
    ts_list.append(y)

    # Compute time delay embedding point clouds
    ptcloud_list.append(takens(y, n=2, tau=4))

Which produces the following figure:

_images/buzz_initialdata.png

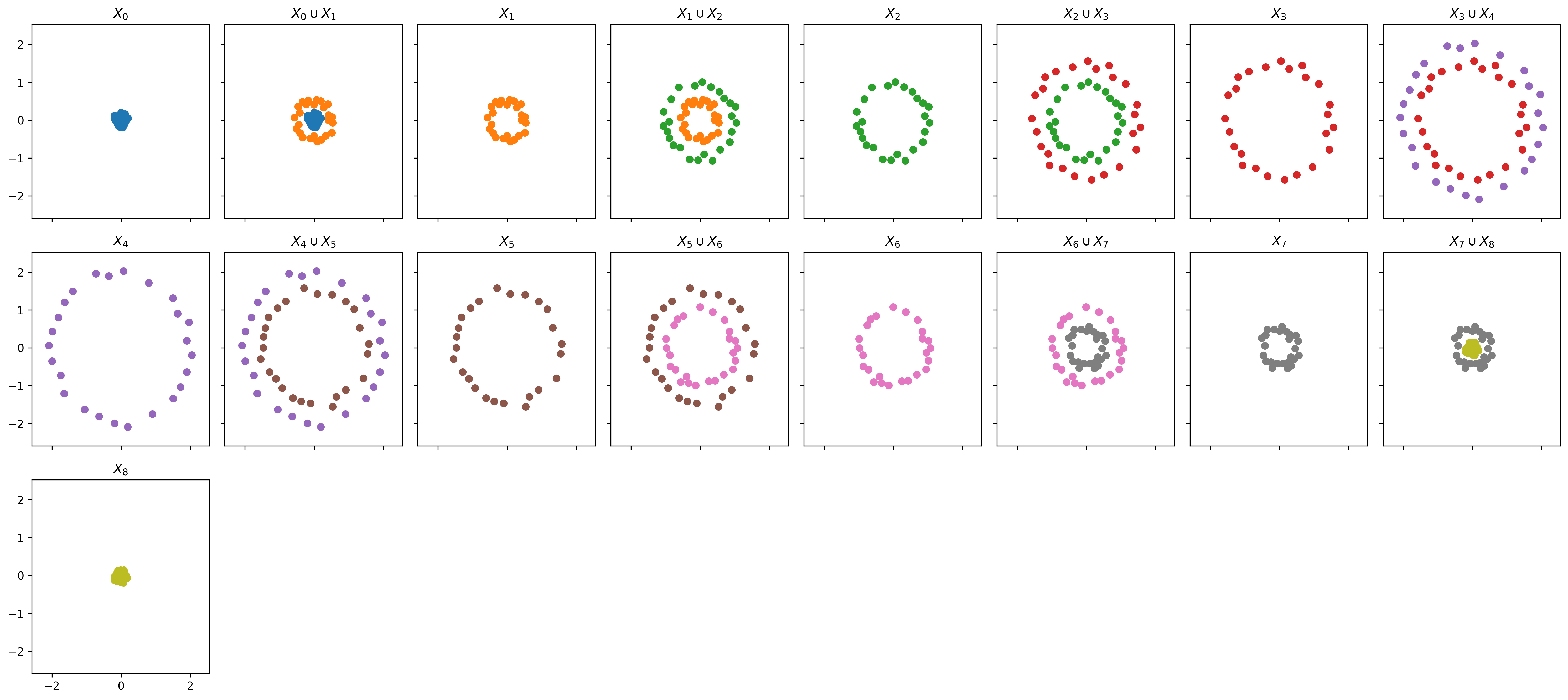
Next, set up the zigzag with the point cloud data, and plot:

# Setup zigzag with point clouds
ZZ = PtClouds(ptcloud_list, num_landmarks=25, verbose=True)

# Plot zigzag of point clouds
ZZ.plot_ZZ_PtClouds()

Which produces the following figure:

_images/buzz_pc_zigzag.png

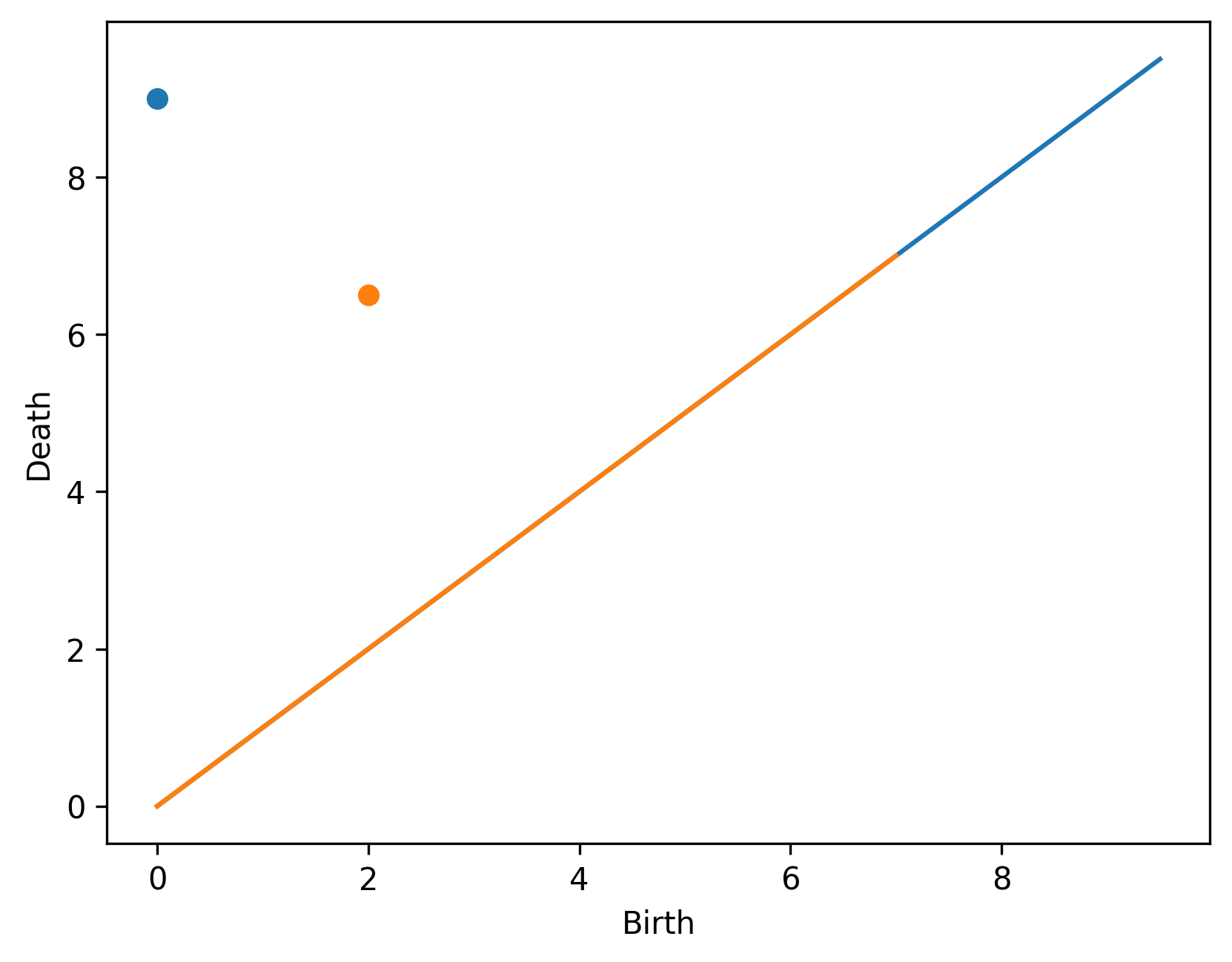
Lastly, compute zigzag persistence, plot the zigzag of resulting Rips complexes and plot the persistence diagrams:

# Compute zigzag persistence
ZZ.run_Zigzag(r=0.85)

# Plot zigzag of Rips complexes
ZZ.plot_ZZ_Cplx()

# Plot zigzag persistence diagram
drawDgm(ZZ.zz_dgms[0]) # 0-dimensional diagram
drawDgm(ZZ.zz_dgms[1]) # 1-dimensional diagram

Which produces the following figures:

_images/buzz_rips_zigzag.png _images/buzz_pd.png